Merkle Tree: How Blockchain Ensures Data Integrity and Security

This article serves as a follow-up to my previous publication on the fundamentals of the Merkle tree.

You can access the previous article by clicking the link below for a comprehensive understanding.

Merkel Tree: What is it, and how does it work?

A Merkle Tree is a binary tree of hash values, where each leaf node represents a single piece of data or a hash of a piece of data. It is used to verify the integrity of large amounts of data efficiently. It was invented by Ralph Merkle in 1979 and is widely used in cryptocurrencies like Bitcoin and Ethereum.

In this article, we will focus on exploring the role of the Merkle tree in the context of blockchain and gaining insights into its integration within the blockchain framework.

Merkle Tree Illustration

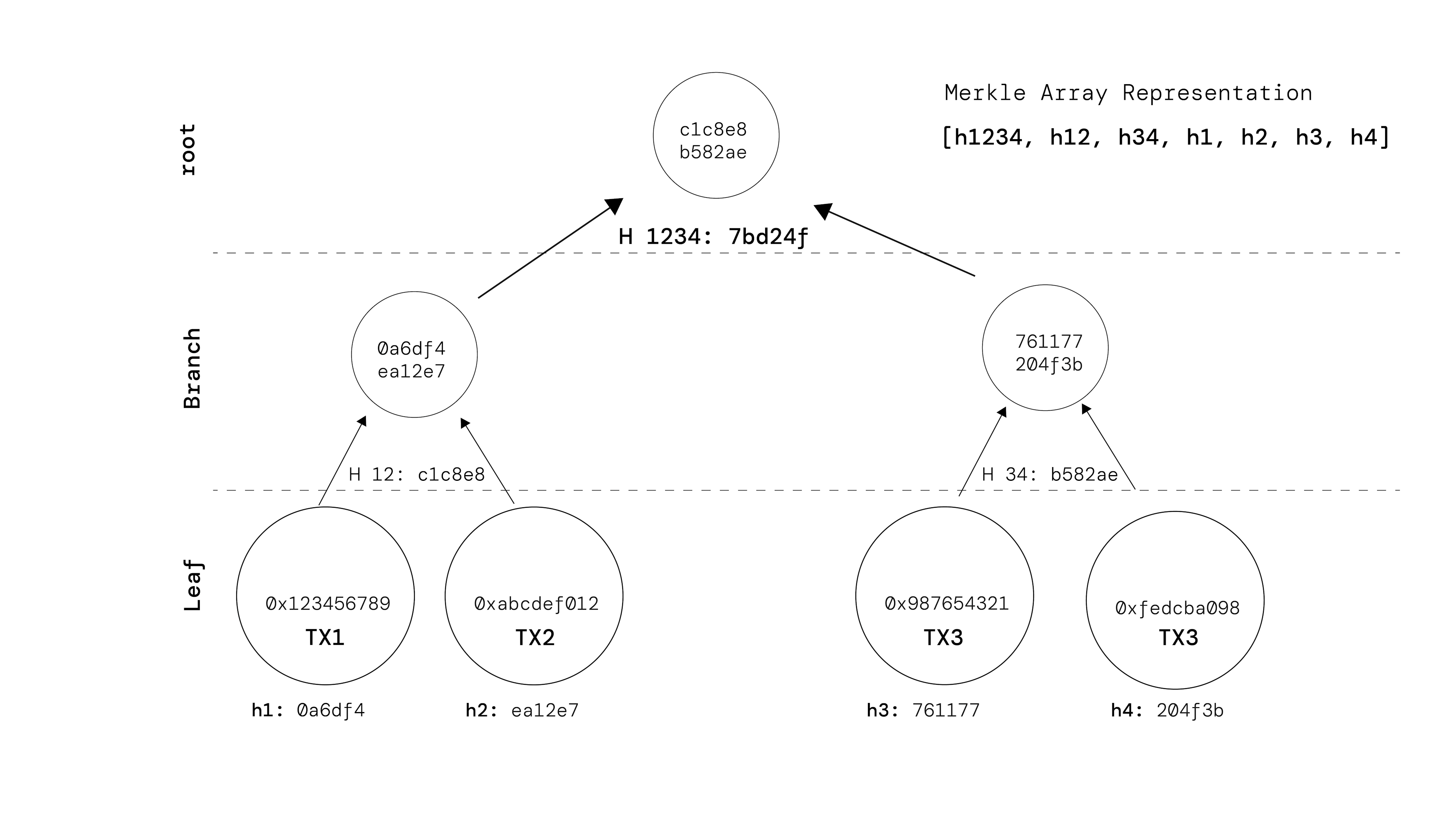
In a blockchain context, a Merkle tree is constructed for the transactions within a block. Let's take an example to illustrate this process. Consider a block containing four transactions:

• Transaction 1: 0x123456789
• Transaction 2: 0xabcdef012
• Transaction 3: 0x987654321
• Transaction 4: 0xfedcba098

To create the Merkle tree, we start by hashing each transaction individually:

• Hash 1 (h1): hash(0x123456789)
• Hash 2 (h2): hash(0xabcdef012)
• Hash 3 (h3): hash(0x987654321)
• Hash 4 (h4): hash(0x123456789)

Next, we combine pairs of hashes and hash them together until we reach the root:

• Hash 12 (H 12): hash(Hash 1 + Hash 2)
• Hash 34 (H 34): hash(Hash 3 + Hash 4)
• Root (H 1234): hash(Hash 12 + Hash 34)

The resulting Merkle root is a unique identifier for the set of transactions within the block. It encapsulates the entire set of transactions and is stored in the block header. By including the Merkle root in the block header, anyone can verify the integrity of the block's transactions by comparing the computed Merkle root with the one stored in the block.

How do the Participants Verify?

Participants do not compute the Merkle root from the ground up during the verification process.Instead, they rely on the Merkle root that is already included in the block header. We'll soon learn who includes it in the block.

When a participant wants to verify a transaction, they typically have access to the block header, which includes the Merkle root. They also have access to the specific transaction they want to verify, along with other necessary information, such as its position within the block (e.g., transaction index or its position in the Merkle tree).

To efficiently verify the transaction, the participant follows these steps:

1. Obtain the necessary hashes: The participant retrieves the relevant hashes required to reconstruct the Merkle path using the transaction data and its position within the block. These hashes include the transaction's immediate parent(s), sibling(s), and any other necessary intermediary hashes.
2. Reconstruct the Merkle path: With the obtained hashes, the participant reconstructs the path from the transaction to the Merkle root by hashing the relevant pairs of hashes iteratively. This process is typically logarithmic in complexity, as the number of hashes required to reconstruct the path is proportional to the height of the Merkle tree.
3. Compare the computed Merkle root: After reconstructing the Merkle path, the participant computes the final Merkle root by hashing the last pair of hashes. They compare this computed Merkle root with the one stored in the block header. If the two values match, it confirms the inclusion and integrity of the transaction within the block.

Who calculates and adds the Merkle root first?

In a blockchain network, the block creator or miner typically performs the process of including the Merkle root in a block. The miner is responsible for assembling the block by including a set of transactions and calculating the corresponding Merkle root.

Here's a high-level overview of the process:

1. Transaction Selection: The miner selects a set of valid transactions to include in the block. These transactions are typically obtained from the network's transaction pool, where pending transactions are stored.
2. Merkle Tree Construction: The miner constructs the Merkle tree by hashing the transactions and combining them until a single Merkle root is obtained. This involves recursively hashing pairs of transaction hashes until reaching the root.
3. Block Assembly: Once the Merkle root is calculated, the miner assembles the block by including the selected transactions, the Merkle root, and other relevant information, such as a timestamp and a nonce.
4. Mining Process: The miner then performs the mining process, which involves repeatedly attempting to find a suitable nonce that satisfies the network's consensus algorithm (e.g., proof-of-work). This process requires significant computational power and aims to find a hash value for the block header that meets specific criteria (e.g., block hash with a certain number of starting zeros, which is defined by the network's difficulty).
5. Broadcasting the Block: Once the miner successfully mines the block by finding a valid nonce, they broadcast the block to the network. At this point, the Merkle root, block header, and other block data become visible to other participants in the network.

After the block is broadcasted, other nodes in the network can independently verify the block's validity. They can calculate the Merkle root using the included transaction hashes and compare it to the Merkle root provided in the block header. If the calculated Merkle root matches the one in the block, the transactions' integrity within the block can be confirmed.

It's important to note that the Merkle root included in the block header is ultimately subject to consensus validation by other nodes in the network. If a block with an invalid Merkle root is detected, it will be rejected by the network, and the consensus algorithm will ensure that only valid blocks are added to the blockchain.

How do participants obtain the required hashes for reconstructing the Merkle path?

Lightweight nodes only keep the block headers and not the whole blocks. This means they don’t know the details of the transactions in each block. They only know the Merkle root, which is a summary of all the transactions. But the Merkle root alone is not enough to check if a specific transaction is in a block. They also need the other hashes that are related to that transaction in the Merkle tree.

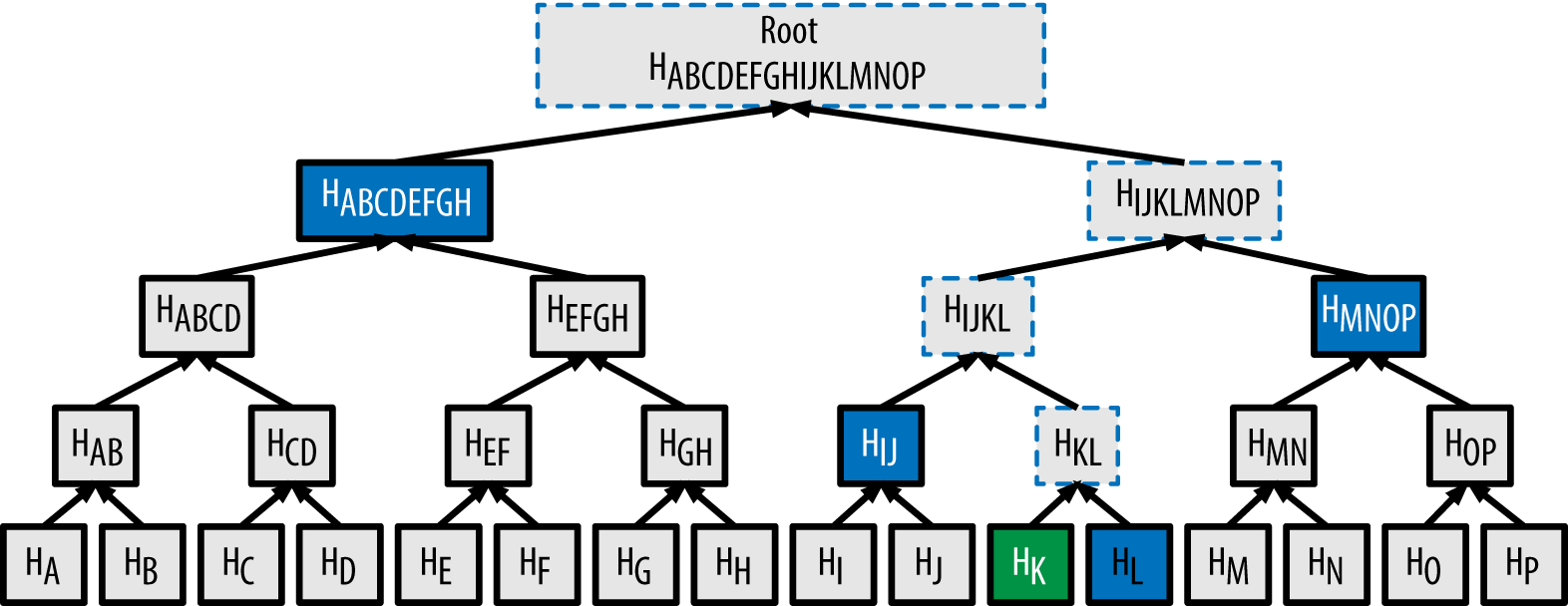
fig 1. Merkle Tree

Any full node that has a complete copy of the block can construct a merkle proof that proves a requested transaction identifier (txid) connects to the merkle root in a block header. Here's an animated graphic showing how Bitcoin Core constructs a merkle proof:

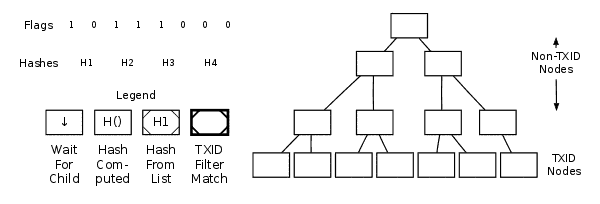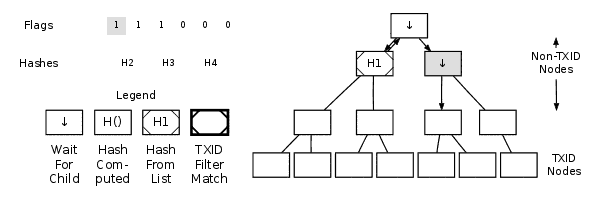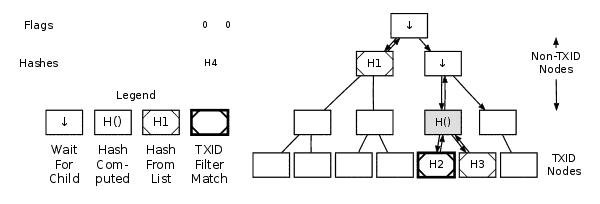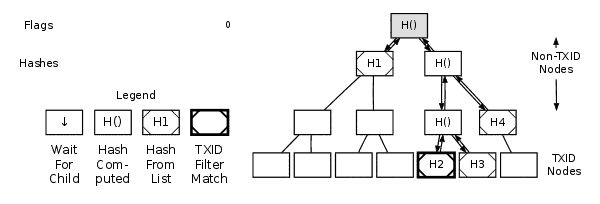
Merkle Tree GIF

For example, if you want to verify that transaction K is in the block, and you have the Merkle tree as shown in the fig 1: You need to ask a full node for the Merkle proof for H_K (the hash of transaction K). The full node will return H_L (the hash of its sibling node), H_IJ (the hash of their parent node), and H_MNOP and H_ABCDEFGH, along with flags indicating which side of each branch they are on. You can then use these hashes and flags to reconstruct the Merkle path and compare it with the Merkle root stored in the block header.

Why not compute the hash of all the Transactions and call it a Root? Why need Merkle Tree?

If we simply compute the hash of all the transactions and call it a root, we lose some important information that the Merkle tree provides. For example:

• We lose the order of the transactions. The Merkle tree preserves the order of the transactions by hashing them in pairs and concatenating them in a specific way. This way, we can verify not only that a transaction is in a block, but also where it is in the block.
• We lose the ability to verify a transaction efficiently. The Merkle tree allows us to verify a transaction by using only a small subset of hashes called the Merkle path or the Merkle proof. If we only have the hash of all the transactions, we need to have all the transactions to verify any one of them.
• We lose the ability to synchronize data efficiently. The Merkle tree allows us to synchronize data between nodes by using only the hashes that are different or missing. If we only have the hash of all the transactions, we need to exchange all the transactions to reconcile any difference or gap in your data.

Therefore, simply computing the hash of all the transactions and calling it a root is not enough to achieve the goals of data verification and synchronization that the Merkle tree enables.

How is the Merkle Tree Represented?

In many implementations, the Merkle tree is represented as an array, often referred to as the Merkle tree array or Merkle tree vector. This representation allows for efficient storage and traversal of the tree structure.

The array representation of the Merkle tree is typically a one-dimensional array that holds all the node hashes, including both the transaction hashes (leaf nodes) and the intermediary hashes (non-leaf nodes). The array is constructed in a way that reflects the hierarchical structure of the binary tree.

The first element of the array is the Merkle root, which is a hash of all the transactions in the block. The rest of the elements are the hashes of the nodes at each level of the tree, from top to bottom and from left to right.

For example, suppose a block has eight transactions (T1 to T8) and their respective hashes (H1 to H8). The array representation of the Merkle tree would look like this:

In this example, H_ABCDEFGH is the Merkle root, which is a hash ofH_ABCD and H_EFGH.H_ABCD is a hash of H_AB and H_CD. H_ABis a hash of H_A and H_B. And so on until the hashes of the transactions (H1 to H8).

Thank you for taking the time to read my article.